The link to the problem: https://leetcode.com/problems/score-after-flipping-matrix/
We have a two-dimensional matrix A where each value is 0 or 1.
A move consists of choosing any row or column and toggling each value in that row or column: changing all 0s to 1s, and all 1s to 0s.
After making any number of moves, every row of this matrix is interpreted as a binary number, and the score of the matrix is the sum of these numbers.
Return the highest possible score.
Conditions:
1 <= A.length <= 201 <= A[0].length <= 20A[i][j]is0or1.
Example
Input: [[0,0,1,1],[1,0,1,0],[1,1,0,0]]
Output: 39
Explanation:
At first, this is our grid:
0 0 1 1
1 0 1 0
1 1 0 0
then if we toggle row 0 ->
1 1 0 0
1 0 1 0
1 1 0 0
then toggle col 2 ->
1 1 1 0
1 0 0 0
1 1 1 0
then toggle col 3 ->
1 1 1 1
1 0 0 1
1 1 1 1
We can get the highest possible score: 1111 + 1001 + 1111 = 15+9+15 = 39Thoughts:
The problem looks hard and it’s kind of clueless to decide which row or which column we should flip. It’s fine, don’t panic! Let’s carefully read our goal —return the highest possible score. Since the final score is the aggregation of the scores in each row, it means that if we want to get the highest score, the score in each row must be as high as possible first.
Since we know that we are going to form a binary number row by row, our first priority is to make the first column of each row 1. Even if the original row is [0,1,1,1…1], the binary number it represents will still less than the row like [1,0,0,….0].
Hence, we will flip all the rows that don’t start with 1. After that, then we can start to add up all the numbers represented by each row. But wait, are we sure that the current sum will be our highest score?
For example, we have a grid that looks like
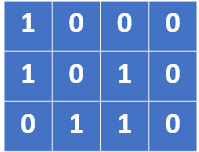
After flipping specific rows —
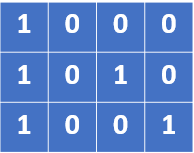
You can see that we only flip the last row since we know that we can’t get a bigger number if we flip the first 2 rows.
If we just look at the above matrix, it is obvious that we should flip some columns to make the final score higher. Hence, our second task is to flip the columns if the 0s are too many in that column. or if we say it more accurately, we will flip the columns in which 0 is the majority.
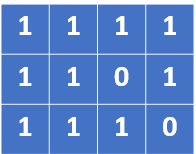
Based on the above idea, we can come up with the code below —
public int matrixScore(int[][] A) {
int m = A.length; //number of rows
int n = A[0].length; //num of cols
//count[i] represents num of 1s in col i
int[] count = new int[n];
//flip row and count 1s in each col
for(int i=0;i<m;i++)
{
boolean flip = A[i][0] == 0;
for(int j=0;j<n;j++)
{
if(flip)
A[i][j] ^= 1;
count[j] += A[i][j];
}
}
int rst = 0;
//calculate rst and also flip col if needed
for(int j=n-1, temp=1;j>=0; j--, temp*=2)
{
int num0 = m - count[j];
if(num0 > count[j]) //flip col
count[j] = num0;
rst += temp* count[j];
}
return rst;
}The above code runs O(m*n+n) time complexity (when we have m rows and n columns). It runs 1ms and beats 37% of submitted codes on Leetcode.
Is it possible that we can improve our current code?
Code Logic:
The reason why we have an extra O(n) time in the above code is that we cannot decide should we flip column j before we traverse all the elements on the column. Since we always traverse each column on each row, we can only know which number (0 or 1) is the majority on a certain column after we traverse all the rows.
However, if we traverse col by col, then we can immediately know whether we need to flip the column before we switch to the next column. We don’t actually need to first traverse the row first since we know the rule of whether flip the row or not depends on the first element in each row.
⚠️The reason why we traverse from the last column to the first column is that we always need to decide whether to flip the current row i depends on the value of A[i][0]. If we traverse from the first column, we will flip the first element of the row and we will need an extra boolean array to record whether we need to flip row i.
Below is the 0ms code that beats 100% —
public int matrixScore(int[][] A) {
int m = A.length; //number of rows
int n = A[0].length; //num of cols
int rst = 0;
for(int j=n-1, temp=1;j>=0;j--, temp*=2)
{
int count = 0;
for(int i=0;i<m;i++)
{
boolean flip = A[i][0]==0; //flip row
if(flip)
A[i][j] ^= 1;
count += A[i][j];
}
//flip col if needed
count = Math.max(count, m-count);
rst += temp * count;
}
return rst;
}